To Study Earth’s Magnetic Field Using Tangent Galvanometer Project PDF Class 12

Introduction
Earth’s magnetic field, also known as the geomagnetic field, is the magnetic field that extends from the Earth’s interior to where it meets the solar wind, a stream of charged particles emanating from the Sun. Its magnitude at the Earth’s surface ranges from 25 to 65 Micro Tesla (0.25 to 0.65 gauss). Roughly speaking it is the field of a magnetic dipole currently tilted at an angle of about 10 degrees with respect to Earth’s rotational axis, as if there were a bar magnet placed at that angle at the centre of the Earth. Unlike a bar magnet, however, Earth’s magnetic field changes over time because it is generated by a geodynamic (in Earth’s case, the motion of molten iron alloys in its outer core).
The North and South magnetic poles wander widely, but sufficiently slowly for ordinary compasses to remain useful for navigation. However, at irregular intervals averaging several hundred thousand years, the Earth’s field reverses and the North and South Magnetic Poles relatively abruptly switch places. These reversals of the geomagnetic poles leave a record in rocks that are of value to paleomagnetic in calculating geomagnetic fields in the past. Such information in turn is helpful in studying the motions of continents and ocean floors in the process of plate tectonics.
The magnetosphere is the region above the ionosphere and extends several tens of thousands of kilometres into space, protecting the Earth from the charged particles of the solar wind and cosmic rays that would otherwise strip away the upper atmosphere, including the ozone layer that protects the Earth from harmful ultraviolet radiation. Earth’s magnetic field serves to deflect most of the solar wind, whose charged particles would otherwise strip away the ozone layer that protects the Earth from harmful ultraviolet radiation.
One stripping mechanism is for gas to be caught in bubbles of magnetic field, which are ripped off by solar winds.
The intensity of the field is often measured in gauss (G), but is generally reported in nanoteslas (nT), with 1 G = 100,000 nT. A nanotesla is also referred to as a gamma (γ). Tesla is the SI unit of the Magnetic field (B). The field ranges between approximately 25,000 and 65,000 nT (0.25–0.65 G).
Near the surface of the Earth, its magnetic field can be closely approximated by the field of a magnetic dipole positioned at the centre of the Earth and tilted at an angle of about 10° with respect to the rotational axis of the Earth. The dipole is roughly equivalent to a powerful bar magnet, with its South Pole pointing towards the geomagnetic North Pole. The north pole of a magnet is so defined because, if allowed to rotate freely, it points roughly northward (in the geographic sense). Since the north pole of a magnet attracts the south poles of other magnets and repels the north poles, it must be attracted to the South Pole.
Tangent Galvanometer
Definition
Tangent galvanometer is the device which was used to measure small amounts of electric current.
Principle
The tangent galvanometer works on the principle of tangent law.
Tangent law of Magnetism
- The tangent law of magnetism states that the tangent of the angle of a compass needle which is due to the movement under the influence of magnetic field is directly proportional to the ratio of strengths of two perpendicular magnetic fields
- In simpler words, the tangent of the angle made by the moving needle under the magnetic field directly indicates the strength of the perpendicular magnetic fields.
Construction
The tangent galvanometer is constructed with a coil of insulated copper wire wound helically around a circular, non-magnetic frame. This helical winding is essential to prevent the magnetic field of the wire from influencing the compass needle, which would lead to errors in readings. The frame is mounted vertically on a horizontal base, and the coil can rotate about a vertical axis through its centre. At the centre of this coil, a small magnetic compass with a strong magnetic needle is pivoted, allowing it to move freely in the horizontal plane. This needle has an aluminium pointer attached at a right angle, enabling precise readings on a circular scale, which is divided into four quadrants (0° to 90° in each). The setup relies on the tangent law of magnetism to function.
Working of Tangent Galvanometer
- The instrument needle starts moving firstly under the influence of Earth’s magnetic field.
- Movement continues until the magnetic field of earth is parallel with the plane of coil.
- Then, on application of an unknown current, a second magnetic field on the axis of the coil which is perpendicular to the Earth’s magnetic field is created.
- Hence the compass needle responds to the vector sum of the two fields.
- This deflection angle is equal to the tangent of the ratio of those two fields.
Application
- G. can be used to measure the magnitude of the horizontal component of the geomagnetic field.
- The principle can be used to compare the galvanometer constants.
- For calibration of secondary instruments.
Apparatus Required
- Tangent Galvanometer
- Commutator
- Rheostat
- Battery
- Ammeter
- Key
THEORY
When a bar magnet is suspended in two magnetic fields B and B_h, it comes to rest making an angle θ with the direction of B_h.
From Figure, B= B_h tanθ This is known as tangent law of magnetism.
If θ is the deflection of the needle, then according to tangent law,
B= B_h tanθ ………. (1)
Let I be the current passing through the coil of radius a with n turns, then the magnetic field generated by the current carrying coil is,
B= (μ_o nI)/2a ……….. (2) (a is the radius of the coil)
Equating (1) and (2) we get,
B_h tanθ= (μ_o nI)/2a ……….. (3)
〖2aB〗_h/(μ_o n) = 1/tanθ ………… (4)
The left-hand side of equation (4) is a constant and is called the reduction factor K of the given Tangent Galvanometer.
K= 1/tanθ …………… (5)
Now from the equation (3) & (5), the horizontal intensity of Earth’s magnetic field B_h is,
B_h= (μ_o nK)/2a …………… (6)
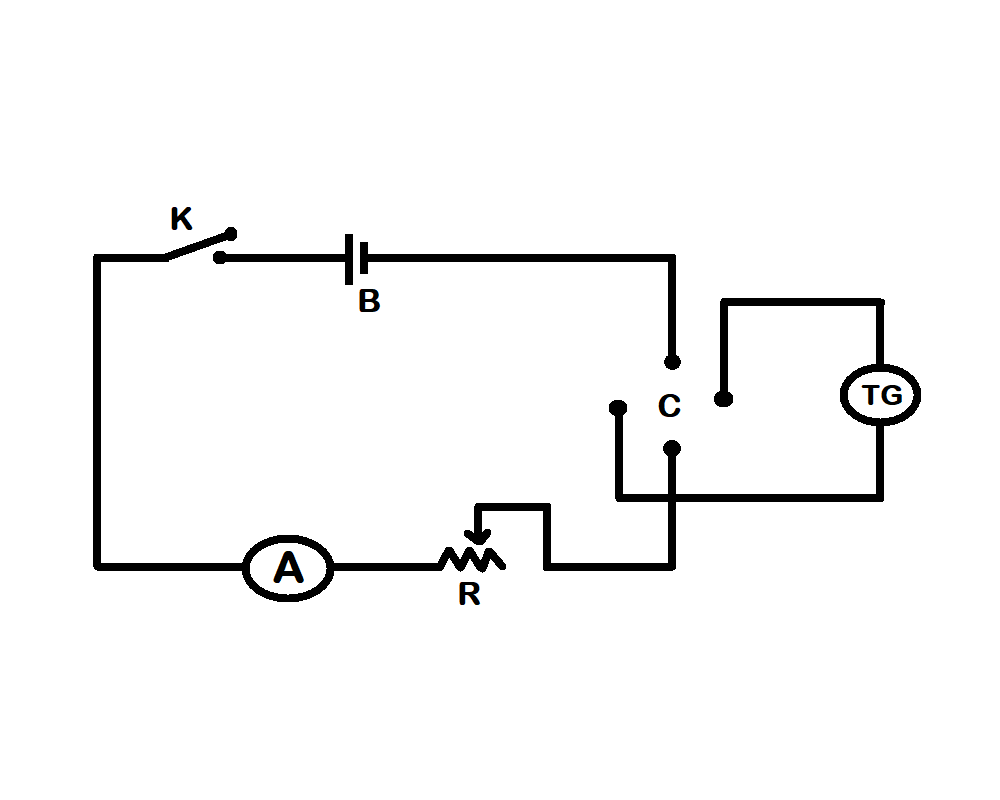
Diagram
Connections are made as shown in the figure given below, where K is the key, E is the battery, A is the ammeter, R is the rheostat, C is the commutator, and T.G is the tangent galvanometer. The commutator can reverse the current through the T.G coil without changing the current in the rest of the circuit. Taking the average of the resulting two readings for deflection averages out any small error in positioning the T.G coil relative to the earth’s magnetic field H.
Procedure
- Make the circuit connections in accordance with the circuit diagram.
- Using spirit level, level the base and the compass needle in compass box of tangent galvanometer by adjusting the levelling screw.
- Now rotate the coil of the galvanometer about its vertical axis, till the magnetic needle, its image in the plane mirror fixed at the base of the compass box and the coil, i.e. all these three lies in the same vertical plane.
- In this setting, the ends of the aluminium pointer should read zero-zero. If this is not so, rotate the box without disturbing the position of the coil till at least one of the ends of the pointer stands at the zero marks.
- By closing the key K, the current flow in the galvanometer. Read the both ends of the pointer. Now reverse the direction of current by using the reversing key. When the mean values of both deflections shown by the pointer in the two cases (i.e. before and after reversing the current) differ by more than , then turn slightly the vertical coil until the two values agree. This will set the plane of the coil exactly in the magnetic meridian.
- By adjusting the rheostat, bring the deflection in galvanometer around . The deflection should not be outside the range.
- Record the reading of the ammeter and the deflection of the compass needle in the box shown by two ends of pointer on the scale.
- Reverse the current in the coil of galvanometer and again record the current and deflection of needle.
- By changing the value of current, take four or more set of readings and plot the graph between I and tan𝜃. The graph will be a straight line.
- Measure the inner and the outer diameter of the coil with a half metre scale at least three times.
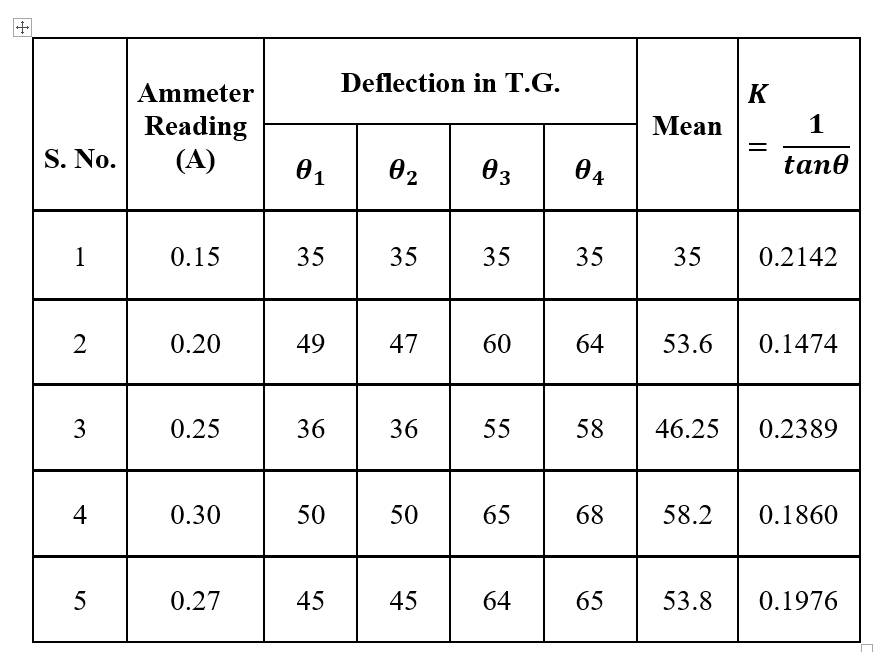
Observation
Calculation
Result
The investigation successfully determined the Earth’s horizontal magnetic field (B_h) using a tangent galvanometer. By varying the current and measuring corresponding deflection angles of the compass needle, the tangent law was applied to calculate the reduction factor (K), which averaged 0.19682. Given 50 turns of the coil with a radius of 8.04 cm, and using the relationship B_h= (μ_o nK)/2a , the Earth’s magnetic field intensity was calculated to be approximately 〖7.6867×10〗^(-8) Tesla. This project effectively demonstrates the use of tangent galvanometry to measure geomagnetic field components with precision.
Conclusion
The project successfully validated the theoretical laws of capacitor combinations. For the parallel configuration, the theoretical capacitance of 1410 μF closely matched the experimental value of 1413.5 μF, confirming that Cp= C1 + C2+ C3 is accurate. In the series configuration, the theoretical capacitance of 156.66 μF was near the experimental value of 153.2 μF, validating the formula
1/Cs = 1/C1 +1/C2 +1/C3 .
Minor differences between theoretical and experimental values are attributed to measurement inaccuracies and component tolerances. Overall, the results support the accuracy of the capacitor combination laws in practical applications.
Precautions
- The battery should be freshly charged.
- The magnetic needle should swing freely in the horizontal plane.
- The plane of coil must be set in magnetic meridian.
- There should be no parallax in noting down the readings of ammeter and deflection.
- All the readings should be adjusted between 30o and 60o.
Sources of Error
- There may a magnetic material around apparatus.
- The plane of coil will not be exactly in the magnetic meridian

