Aim

To verify that 63% charge is stored in a capacitor in a R-C circuit at its time constant and 63% charge remains when capacitor is discharged and hence plot a graph between voltage and time.

Introduction

An R-C circuit is a circuit containing a resistor and capacitor in series to a power source. Such circuits Find very important applications in various areas of science and in basic circuits which act as building blocks of modern technological devices.

It should be really helpful if we get comfortable with the terminologies charging and discharging of capacitors.

1. 1. Charging of Capacitor: –

A capacitor is a passive two-terminal electrical component used to store energy in an electric field. In the hydraulic analogy, charge carriers lowing through a wire are analogous to water flowing through a pipe. A capacitor is like a rubber membrane sealed inside a pipe. Water molecules cannot pass through the membrane, but some water can move by stretching the membrane. The analogy clarifies a few aspects of capacitors:

 

• • The low of current alters the charge on a capacitor, just as the low of water changes the position of the membrane. More specifically, the effect of an electric current is to increase the charge of one plate of the capacitor, and decrease the charge of the other plate by an equal amount. This is just like how, when water low moves the rubber membrane, it increases the amount of water on one side of the membrane, and decreases the amount of water on the other side.

 

• • The more a capacitor is charged, the larger its voltage drop; i.e., the more it “pushes back” against the charging current. This is analogous to the fact that the more a membrane is stretched, the more it pushes back on the water.

 

• • Current can low “through” a capacitor even though no individual electron can get from one side to the other. This is analogous to the fact that water can low through the pipe even though no water molecule can pass through the rubber membrane. Of course, the low cannot continue the same direction forever; the capacitor will experience dielectric breakdown, and analogously the membrane will eventually break.

 

• • The capacitance describes how much charge can be stored on one plate of a capacitor for a given “push” (voltage drop). A very stretchy, flexible membrane corresponds to a higher capacitance than a stiff membrane.

 

• • A charged-up capacitor is storing potential energy, analogously to a stretched membrane.

 

• • Discharging of Capacitor: –

Using hydraulic analogy only we can understand that when the capacitor is charged the membrane is stretched, but now if you allow the water to come out slowly and let the membrane relax, then it is called discharging of capacitor. In other words, when the charge on each of the plates becomes zero and the potential difference across its terminals drops to zero.

Material Required

Materials Required: –

 

1. 1. Breadboard

 

• • 100µF capacitor

 

• • 1 MΩ resistor

 

• • Multi-meter

 

• • 9V battery

 

• • Wire stripper, connecting wires, battery connector

 

• • Stopwatch

Theory

Procedure

 

• • Connect all the components in breadboard

 

• • Now take multimeter leads and place them in the two terminals

 

• • Now take the Battery and its terminal across the terminal of the capacitor and start the stopwatch. Note the readings at 20sec intervals and write them down. [NOTE: – Reading the previous statement could be astonishing as it says that measure voltage at 20sec interval but one could question that current move at very high speed so how could one measure the changing readings! But believe me it wasn’t an easy task but since the voltage depends on reciprocal of exponential function and as time passes by the changing readings will get slowed down and even after infinite time the capacitor could not be charged up to max voltage. Also, since its time constant is 100sec which is quite practical to measure at and hence this experiment is very much justified.]. Take 10 readings and if required the 20sec gap could be increased because as the time passes by the change in voltage becomes smaller and smaller.

 

• • Now let the capacitor be charged up to 460 secs because then it will become 99.99% charged [since we have a limited time and we can’t wait for infinite time for it to charge completely. Now remove the battery and now attach a wire in place of the battery terminals and again note the multimeter readings changing and record them.

 

• • Plot a graph between voltage and time for charging as well as discharging

Observation

S No.	Multi-meter reading while charging (in V)	Multi-meter reading while discharging (in V)	Time (in S)
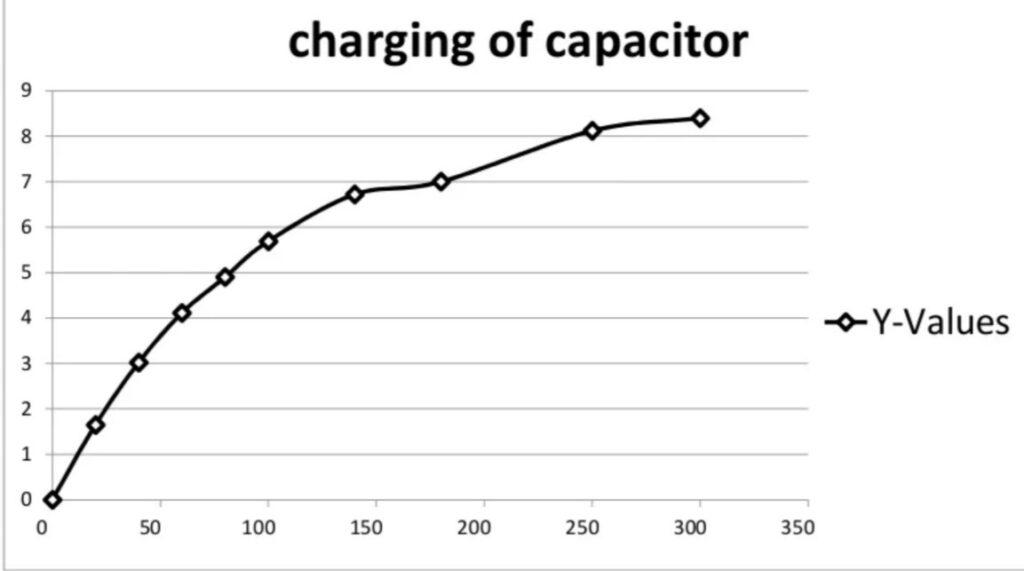
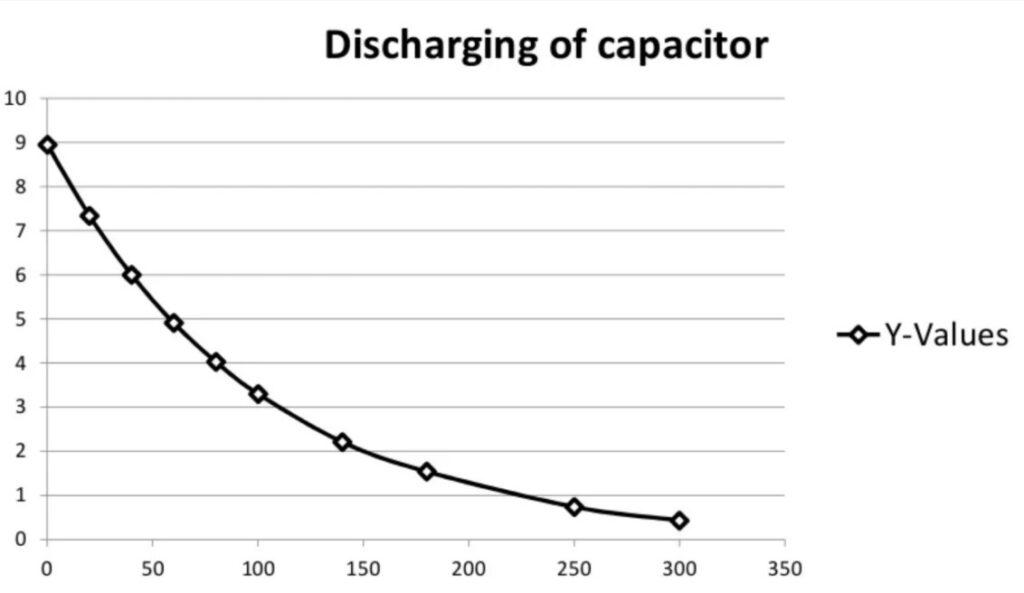
1	0	8.95	0
2	1.65	7.34	20
3	3.02	6.00	40
4	4.11	4.91	60
5	4.90	4.03	80
6	5.69	3.30	100
7	6.72	2.21	140
8	7.00	1.54	180
9	8.12	0.74	250
10	8.40	0.43	300

Graphical Representation

Plot of voltage vs time

Time on X-axis and Voltage on Y-axis

 

• • For Charging

 

• • For Discharging

     

    • •  

Calculation

Now since the Graph are very much similar to the graph of charging and discharging of capacitor.

At τ=100s, during charging of capacitor the voltage on capacitor is 5.69 volt as it is observed in the experiment. Now using the charging formula:

V= 9(1-e^-t/t)
V= 9(1-1/e)
V= 5.67 ~ 5.69
Which is achieved experimentally as well.

Similarly, during discharging,
V= 9-e^-1
V= 3.32 ~ 3.30

Which is achieved experimentally as well.

Conclusion

Hence it is verified experimentally that 63% charge is there on capacitor after time constant during charging and 63% charge is lost at time constant during discharging.

Precaution

 

• • Do all the connection carefully

• • Do all the connection neat and tight

• • Do not connect Led without resistance

• • Keep yourself safe from high voltage

• • Before doing any experiment please consult to your subject teacher or lab assistance

Bibliography

 

• • Wikipedia.com

• • Google search engine

• • WWW.YOUTUBE.COM

• • Physics NCERT book for class XII